Sri Lanka Schools AL ICT Logic Gates to design basic digital circuits and devices (ICT Grade 12 Lesson 4 ). After studying this chapter, you will be able to understand the following:
- Analyzes basic digital logic gates in terms of their unique functionalities.
- Simplifies logic expressions using laws of Boolean algebra and Karnaugh map.
- Designs simple digital circuits using logic gates.
- Explores how combinational logic circuits are used in CPU and sequential circuits in physical memory.
You can get better practical knowledge by watching the given videos related to the topics mentioned in the syllabus of this lesson AL ICT Logic Gates. By clicking on the relevant categories, you can see the description of the lesson related to the topic
? Learning Video Option 1 – Sinhala Medium – Play List Included 15 Videos with Question discussion
-

04 වන ඒකකය | 03 වන පාඩම - අංකිත පරිපථ වල බිටු ගබඩා කිරිම - 02 වන කොටස Al ICT
-

04 වන ඒකකය | 03 වන පාඩම - මධ්ය සැකසුම් ඒකකයේ හා භෞතික මතකයේ තැනුම් ඒකක - 01 වන කොටස Al ICT
-

04 වන ඒකකය | 03 වන පාඩම -2018 AL ප්රශ්ණ සකච්චාව - 03 වන කොටස Al ICT
-

04 වන ඒකකය | 04 වන පාඩම - තාර්කික ද්වාර සමාලෝචන ප්රශ්ණ - 01 වන කොටස Al ICT
-

04 වන ඒකකය | 04 වන පාඩම - තාර්කිකා ද්වාර - 03 වන කොටස | AL IT Unit 04
-

04 වන ඒකකය | 04 වන පාඩම - තාර්කිකා ද්වාර - 02 වන කොටස | AL IT Unit 04
-

04 වන ඒකකය | 02 වන පාඩම - තාර්කික ද්වාර - 05 වන කොටස | AL IT Unit 04 Lesson 2
-

04 වන ඒකකය | 02 වන පාඩම - තාර්කික ද්වාර - 02 වන කොටස | AL IT Unit 04 Lesson 2
Given below is an AL ICT resources Book prepared in relation to your syllabus.
For an enlarged view of the resources Book, ? Click Here
Related resources and links to this lesson
External Links
online logic gate drawing tool at ? (https://logic.ly/demo/)
Dynamic Truth Table Generator
AL ICT Logic Gates: Understanding the Fundamentals of Digital Logic
In the world of digital electronics, logic gates play a fundamental role in processing and manipulating binary data. These gates form the building blocks of complex digital circuits, enabling computers and electronic devices to perform various operations and tasks. This article aims to provide a comprehensive understanding of AL ICT logic gates, their functionalities, simplification techniques, and practical applications in designing digital circuits.
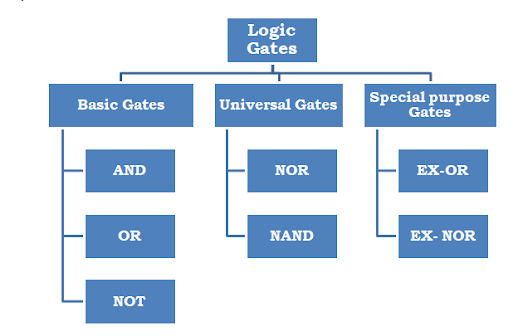
1. AL ICT Logic Gates
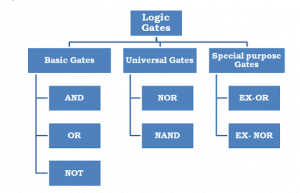
Logic gates are electronic devices that operate on binary inputs (0s and 1s) to produce binary outputs based on predefined logical functions. These gates are implemented using transistors and can be categorized into several types, such as AND gates, OR gates, NOT gates, XOR gates, and more. By combining these basic gates, complex digital circuits can be constructed to perform a wide range of operations.
2. Understanding Boolean Algebra
Boolean algebra is a mathematical system that deals with binary variables and logical operations. It provides a set of rules and laws to manipulate and simplify logic expressions. With Boolean algebra, complex logical problems can be broken down into simpler components, allowing for easier analysis and optimization of digital circuits.
3. The Fundamental Logic Gates
3.1. AND Gate
The AND gate is one of the most fundamental logic gates. It takes two binary inputs and produces an output that is only HIGH (1) when both inputs are HIGH; otherwise, the output is LOW (0). The AND gate can be represented by the Boolean expression: A AND B = Y.
3.2. OR Gate
The OR gate is another essential logic gate. It also takes two binary inputs but produces an output that is HIGH if at least one of the inputs is HIGH. The output is LOW only when both inputs are LOW. The Boolean expression for the OR gate is: A OR B = Y.
3.3. NOT Gate
The NOT gate, also known as an inverter, has a single input and produces the opposite value as its output. If the input is HIGH, the output is LOW, and vice versa. It can be represented by the expression: NOT A = Y.
3.4. XOR Gate
The XOR (exclusive OR) gate takes two binary inputs and produces a HIGH output when the number of HIGH inputs is odd. In other words, the output is HIGH if the inputs are different. If both inputs are the same, the output is LOW. The XOR gate can be expressed as A XOR B = Y.
4. Logic Gate Combinations and Truth Tables
By combining different logic gates, complex logic functions can be implemented. The behavior of these combinations can be described using truth tables, which show the output for all possible input combinations. Truth tables provide a concise representation of logic gates’ functionalities and help in understanding and designing complex digital circuits.
5. Simplifying Logic Expressions with Boolean Algebra
Boolean algebra offers a set of rules and laws that allow the simplification of logic expressions. By applying these rules, complex expressions can be reduced to their simplest form, enabling more efficient circuit design. The laws of Boolean algebra include commutative, associative, distributive, identity, complement, and absorption laws.
6. Simplifying Logic Circuits using Karnaugh Maps
Karnaugh maps, also known as K-maps, are graphical tools used to simplify logic expressions further. They provide a systematic approach to finding the minimal expression by grouping adjacent 1s in the map. K-maps offer a visual representation that aids in simplifying complex logic functions and reducing the number of gates required in a circuit.
7. Designing Digital Circuits with Logic Gates
Logic gates serve as the building blocks for designing digital circuits. By combining different gates and applying simplification techniques, complex circuits can be constructed to perform specific tasks. Designing digital circuits requires careful consideration of gate combinations, input/output requirements, and overall functionality.
8. Application of Logic Gates in CPUs
Logic gates are extensively used in central processing units (CPUs) to perform arithmetic and logical operations. The ALU (Arithmetic Logic Unit) within a CPU consists of various logic gates that enable calculations, comparisons, and data manipulations. The efficient implementation of logic gates in CPUs is crucial for the overall performance and functionality of computers and electronic devices.
9. Sequential Circuits and Physical Memory
In addition to combinational logic circuits, sequential circuits play a vital role in digital electronics. Sequential circuits contain memory elements that enable them to store and process data based on previous inputs. These circuits are used in physical memory units, registers, and other components to facilitate data storage, retrieval, and processing.
10. Conclusion
Logic gates form the backbone of digital electronics, allowing for the creation of complex circuits that power our modern technology. Understanding the different types of logic gates, their functionalities, simplification techniques, and practical applications is essential for anyone working in the field of digital logic design. By applying Boolean algebra, utilizing Karnaugh maps, and implementing logic gates effectively, engineers can design efficient and reliable digital circuits for various applications.
FAQs
Q1: Are there logic gates other than the ones mentioned in this article? Yes, there are other types of logic gates, such as NAND gates, NOR gates, XNOR gates, and more. They are derived from combinations of the fundamental gates discussed in this article.
Q2: Can logic gates be used in non-electronic systems? While logic gates are primarily used in electronic systems, their concepts can be applied to non-electronic systems as well. The principles of binary logic and Boolean algebra can be used in fields like computer science, mathematics, and even decision-making processes.
Q3: Is it possible to build complex circuits using only one type of logic gate? Yes, it is possible to build complex circuits using a single type of logic gate. For example, a circuit constructed solely with NAND gates can perform any logical function. This concept, known as NAND universalism, demonstrates the versatility of logic gates.
Q4: How do logic gates contribute to energy efficiency in digital systems? Logic gates play a crucial role in energy-efficient digital systems. By optimizing the design and minimizing the number of gates used, power consumption can be reduced. Additionally, advanced techniques like clock gating and power gating are employed to further enhance energy efficiency.
Q5: Can I learn more about designing digital circuits and logic gates? Certainly! There are numerous online resources, books, and tutorials available that delve deeper into the world of digital logic design.
In conclusion, AL ICT logic gates are the fundamental components of digital circuits. They enable the processing and manipulation of binary data, simplify logic expressions, and facilitate the design of complex digital systems. Understanding the functionalities of different logic gates, employing Boolean algebra and Karnaugh maps for simplification, and applying these concepts in circuit design are essential skills for anyone working in the field of digital logic. By harnessing the power of logic gates, engineers can create efficient and reliable digital circuits that drive technological advancements in various industries.






















Leave a Reply