Number Systems: Grade 8 ICT Lesson 1

Understanding number systems is an essential skill for any budding computer scientist or ICT enthusiast. Number systems form the foundation of how computers process and store data. In this blog post, we’ll explore the fundamental concepts of number systems, their symbols, bases, and how to perform conversions between different systems. Let’s dive in!

You can get better practical knowledge by watching the given videos related to the topics mentioned in the syllabus of this lesson Grade 8 ICT – By clicking on the relevant categories, you can see the description of the lesson related to the topic

Related resources and links to this lesson

Text Book  Work Book 

What is a Number System?

A number system is a way of representing numbers using specific symbols and rules. Humans use numbers for counting, calculating, and measuring. Computers, however, use a unique numbering system called the binary number system to process information.

Symbols and Base of a Number System

Every number system is defined by:

1. Symbols: The digits used to represent numbers.
2. Base (or Radix): The total number of unique symbols in the system.

The Binary Number System

The binary system is a base-2 number system that uses only two symbols: 0 and 1. Computers use binary because electronic circuits have two states: ON (1) and OFF (0). Every piece of data a computer processes, from text to images, is represented in binary.

Why is Binary Important?

• Used in all modern computing systems.
• Forms the basis for data representation and processing.

The Decimal Number System

The decimal system is a base-10 number system that uses ten symbols (0 through 9). This is the number system humans use daily for calculations, money, and measurements.

Converting Between Decimal and Binary

1. Converting Decimal to Binary

To convert a decimal number into binary, follow these steps:

1. Divide the decimal number by 2.
2. Record the remainder (0 or 1).
3. Divide the quotient by 2 and repeat until the quotient becomes 0.
4. Write the remainders in reverse order to get the binary equivalent.

Example: Convert 13 to Binary

• 13 ÷ 2 = 6 remainder 1
• 6 ÷ 2 = 3 remainder 0
• 3 ÷ 2 = 1 remainder 1
• 1 ÷ 2 = 0 remainder 1
  Binary equivalent: 1101

2. Converting Binary to Decimal

To convert a binary number into decimal:

1. Write down the binary number.
2. Multiply each binary digit by 2 raised to the power of its position (starting from 0 on the right).
3. Add the results.

Example: Convert 1101 to Decimal

• (1×23)+(1×22)+(0×21)+(1×20)(1 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0)(1×23)+(1×22)+(0×21)+(1×20)
• 8+4+0+1=138 + 4 + 0 + 1 = 138+4+0+1=13
  Decimal equivalent: 13

Representation of Data Using the Binary Number System

Computers store and process all types of data using binary. Here’s how different types of data are represented:

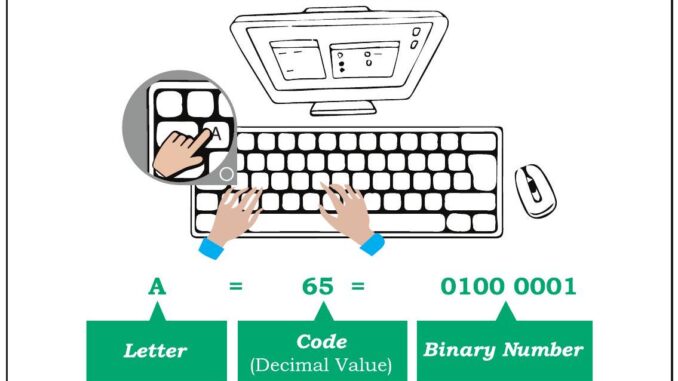
• Text: Each character is assigned a binary code using systems like ASCII (e.g., ‘A’ = 01000001).
• Images: Images are stored as binary values for each pixel’s color.
• Audio: Sounds are digitized into binary values.

Advantages of Binary Data Representation

• Reliable for digital systems with ON/OFF states.
• Easy to implement with electronic circuits.

Why Learn About Number Systems?

Understanding number systems is crucial for:

1. Programming: Binary is the language of computers.
2. Data Storage: Knowing how data is stored helps you optimize storage and processing.
3. ICT Skills: Essential for advanced topics like logic gates, algorithms, and computer architecture.

Practice Questions

1. Convert the decimal number 25 to binary.
2. Convert the binary number 10101 to decimal.
3. What is the base of the hexadecimal number system?
4. Why do computers use the binary number system?
5. How is text data represented in binary?

By mastering these basics of number systems, you’re taking your first steps into the world of computing. Keep practicing conversions, and you’ll soon find these concepts easy and intuitive.

FAQs

1. What is the base of the binary number system?
The binary system has a base of 2.

2. Why do computers use binary?
Binary is used because it aligns with the ON/OFF states of electronic circuits.

3. How do I convert a binary number to decimal?
Multiply each binary digit by 2 raised to its position, then sum the results.

4. What is the difference between binary and decimal systems?
The binary system uses only two digits (0, 1) and has a base of 2, while the decimal system uses ten digits (0-9) with a base of 10.

5. Can I convert binary to other number systems like octal or hexadecimal?
Yes! You can group binary digits to simplify conversions to octal (group by 3s) or hexadecimal (group by 4s).