1.Using the given logic circuit with inputs A, B, and C, construct the truth table to determine the output Q for all possible input combinations.
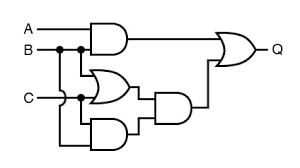
2. The given logic circuit has inputs A (door sensor), B (window sensor), and C (motion sensor), and output Q (alarm). Describe a real-world scenario where this circuit would trigger the alarm, and explain the conditions under which the alarm will sound based on the circuit’s logic.
1.
Answer:
Let’s break down the circuit:
- First AND gate (A and B): Output = A ∧ B
- Second AND gate (Output of first AND gate and C): Output = (A ∧ B) ∧ C
- OR gate (Output of first AND gate and second AND gate): Q = (A ∧ B) ∨ ((A ∧ B) ∧ C)
Truth table:
| A | B | C | A ∧ B | (A ∧ B) ∧ C | Q = (A ∧ B) ∨ ((A ∧ B) ∧ C) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Description: To solve this, students need to evaluate the circuit step-by-step: first, compute the output of the first AND gate (A ∧ B), then use that output with C in the second AND gate, and finally combine the results using the OR gate. The truth table shows that Q is 1 only when A and B are both 1, regardless of C, due to the OR gate’s logic. This exercise reinforces how to trace signals through a circuit and build a truth table, a key skill in Competency Level 4.1.
2.
Answer:
Scenario: This circuit can be used in a home security system where the alarm (Q) should trigger if both the door (A) and window (B) sensors are activated, regardless of the motion sensor (C).
Conditions: The alarm will sound (Q = 1) when:
- A = 1 and B = 1 (both door and window sensors are triggered), regardless of C.
From the circuit: - The first AND gate (A ∧ B) outputs 1 only if both A and B are 1.
- The second AND gate ((A ∧ B) ∧ C) outputs 1 only if A, B, and C are all 1.
- The OR gate outputs Q = 1 if the first AND gate outputs 1 (i.e., A ∧ B = 1), meaning the alarm triggers whenever A and B are both 1, regardless of C’s value.
For example:
- If A = 1, B = 1, C = 0 (door and window open, no motion), the alarm will sound.
- If A = 1, B = 1, C = 1 (door, window, and motion all detected), the alarm will still sound.
- If A = 0, B = 1, C = 1 (only window and motion detected), the alarm will not sound because A ∧ B = 0.
Description: This question connects the circuit to a practical scenario, helping students apply Boolean logic to real-world problems as outlined in Competency Level 4.2. The circuit’s logic shows that the alarm depends only on the door and window sensors being activated together, teaching students how to interpret logic circuits in context. It also encourages critical thinking about how sensor inputs can control outputs in security systems.
