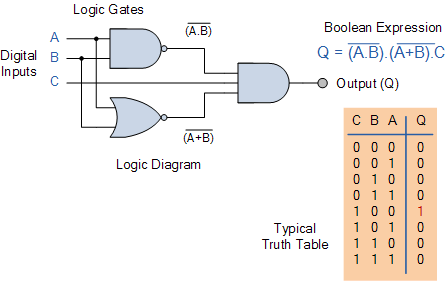
Sri Lanka school ICT – Grade 10 Lesson 4 is Logic Gates with Boolean Functions. After studying this chapter, you will be able to understand the following:
- signals used in electronic science
- basic logic gates and combinational logic gates
- representing Boolean expressions using truth tables
- creating combinational logic gates based on basic logic gates
- drawing digital circuits for Boolean expressions
- Constructing truth tables after writing Boolean expressions for digital circuits
- Integrated Circuits
- practical usage of logic gate
You can get better practical knowledge by watching the given videos related to the topics mentioned in the syllabus of this lesson. By clicking on the relevant categories, you can see the description of the lesson related to the topic
? Learning Video Option 1 – Sinhala Medium – Play List Included 6 Videos with Question discussion
-

5 වන පාඩම | මෙහෙයුම් පද්දති - 4 වන කොටස | තොරතුරු හා සන්නිවේදනය | 10 වන ශ්රේණිය
-

5 වන පාඩම | මෙහෙයුම් පද්දති - 3 වන කොටස | තොරතුරු හා සන්නිවේදනය | 10 වන ශ්රේණිය
-

5 වන පාඩම | මෙහෙයුම් පද්දති - 2 වන කොටස | තොරතුරු හා සන්නිවේදනය | 10 වන ශ්රේණිය
-

5 වන පාඩම | මෙහෙයුම් පද්දති - 1 වන කොටස | තොරතුරු හා සන්නිවේදනය | 10 වන ශ්රේණිය
Given below is a series of notes prepared in relation to your syllabus.
For an enlarged view of the Note ? Click Here
Related resources and links to this lesson
Text Book Lesson Note Download Questions MCq
external resources
online logic gate drawing tool at ? (https://logic.ly/demo/)
http://15.235.229.3/~schoolic/dynamic-truth-table-generator/
Communication happens in various ways among living beings in day-to-day life. Drumming was used in the past, as a method of communication. Further, a railway guard in a station blows a horn waving a green flag to signal that a train is going to leave. A green light should be there for the train to start and if it is a red light, the signal is to stop.
Usually, two keys are used to open a safe and both keys are needed to open it. Before you start a journey in a car, all its doors should be closed properly. If at least one door is not closed properly, a light will be on or there will be a sound for the driver to signal it. When all the doors are closed, this signal will be stopped. Further, you should wear seat belts if you are seated in the front seat of a car.
Otherwise, there will be a signal to indicate this. Thus, as we use signals in our day-to-day life to make decisions, the computer also uses signals.
Learning Video – English Medium
Learning Video – Tamil Medium
Basic Logic Gates in Computer Science
Basic Logic in Computer Science: A Guide to Understanding and Utilizing Boolean Algebra
Computer Science is a field that heavily relies on the use of basic logic for solving problems and developing algorithms. The basic logic is the foundation of digital electronics and computer science and is used in a wide range of applications, from designing digital circuits to implementing decision-making algorithms in programming. In this article, we will explore how basic logic is used in computer science and why it is an essential aspect of the field.
Representing and Solving Problems using Boolean Algebra
Boolean algebra is a mathematical system that uses binary values, 0 and 1, to represent true and false. It provides a way to model and analyze problems using basic logic operations such as AND, OR, NOT, NAND, and NOR. Boolean algebra is used to simplify complex expressions and to design digital circuits. For example, using Boolean algebra, it is possible to represent a complex problem, such as a traffic light system, as a series of simple logical operations. This makes it easier to analyze the problem and design a solution.
Designing Digital Circuits using Basic Logic Gates
Basic logic gates are the building blocks of digital circuits. They take binary inputs and produce binary outputs based on the logical operation performed. The most common basic logic gates are NOT, AND, OR, NAND, and NOR. These gates can be combined to create more complex digital circuits that can perform various functions such as decision-making, arithmetic operations, and data storage. For example, a combination of AND, OR, and NOT gates can be used to design a circuit that performs a specific arithmetic operation, such as addition or subtraction.
Creating Decision-Making Algorithms and Control Flow Structures in Programming
In computer programming, the basic logic is used to implement decision-making algorithms and control flow structures. If-else statements and switch-case statements are examples of control flow structures that use basic logic operations. These structures allow the programmer to control the flow of execution of a program based on certain conditions. For example, an if-else statement can be used to check if a certain condition is met, and if it is, the program will execute a specific set of instructions. This is a crucial aspect of programming and is used extensively in developing algorithms and solving problems.
Implementing Error Detection and Correction Codes
Error detection and correction codes are used in computer systems to detect and correct errors that may occur during data transmission or storage. These codes make use of basic logic operations to generate redundancy in the data, which can be used to detect and correct errors. For example, using basic logic operations, it is possible to generate a parity bit that can be used to detect errors. If an error is detected, the correction code can be used to correct the error, ensuring that the data is transmitted or stored accurately.
Developing Binary Arithmetic Operations and Understanding the Basics of Computer Arithmetic
Binary arithmetic is the foundation of computer arithmetic. It involves performing arithmetic operations on binary numbers and provides a way to understand how computers perform arithmetic operations. Basic logic gates can be used to implement binary arithmetic circuits, such as adders and subtractors. Understanding the basics of binary arithmetic is essential for computer scientists, as it provides a deeper understanding of how computers perform arithmetic operations and how to design algorithms that perform arithmetic operations efficiently.
Utilizing Truth Tables and Karnaugh Maps for Simplifying Boolean Expressions
Truth tables and Karnaugh maps are useful tools for simplifying Boolean expressions. A truth table provides a way to visualize the output of a Boolean expression for all possible input combinations. A Karnaugh map is a graphical representation of a truth table and provides a way to simplify Boolean expressions by identifying adjacent 1’s





ගොඩක් හොද වැඩක්
නියමයි සර්. ඒ
මෙහි හැම පාඩමක් ම තියෙනවා.